The tips dataset contains data on tip size collected from one waiter over a couple of months. we will create an additional variable log_tips, which will be the log of the tip size for each meal.
data(tips) tips$log_tips <- log(tips$tip)
We move tip and log_tips to the right hand list. We select the shapiro-wilk test, and deselect the t-test. We will also plot some histograms to visualize the data, so in the plot dialog we select that we wish to produce a plot, and deselect box plot and Scale variables.
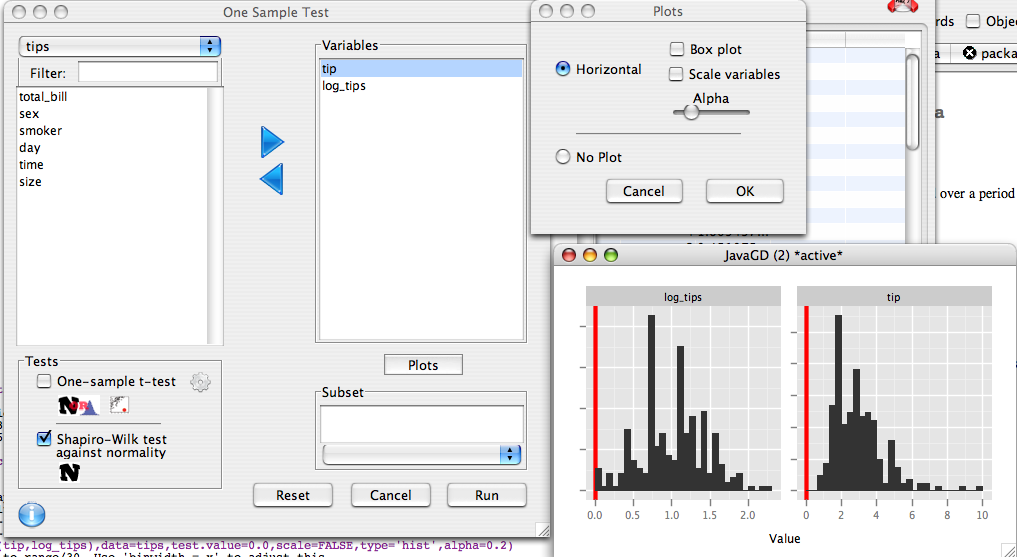
This produces the following code:
descriptive.table(vars=d(tip,log_tips),data=tips,func.names =c("Mean","St. Deviation","Valid N"))
one.sample.test(variables=d(tip,log_tips),
data=tips,
test=shapiro.test)
onesample.plot(variables=d(tip,log_tips),data=tips,type='hist',alpha=0.2)
> descriptive.table(vars=d(tip,log_tips),data=tips,func.names =c("Mean","St. Deviation","Valid N"))
$`strata: all cases `
Mean St. Deviation Valid N
tip 2.998279 1.3836382 244
log_tips 1.002538 0.4361609 244
> one.sample.test(variables=d(tip,log_tips),
+ data=tips,
+ test=shapiro.test)
Shapiro-Wilk normality test
W p-value
tip 0.8978112 8.200597e-12
log_tips 0.9888472 5.621705e-02
> onesample.plot(variables=d(tip,log_tips),data=tips,type='hist',alpha=0.2)
We can see that tip is highly skewed, and is definitely not normal. The shapiro-wilk p-value is 8.200597e-12 or .0000000000082. By contrast, when we log transform the tips, the p-value is not significant (0.056), and the histogram looks roughly symmetrical.