This example will use the tips dataset, which records the tips a waiter got over a period of a couple months. In a previous example we found that tips was rather skewed, so we will also examine log(tips).
Enter the following into the console:
data(tips) tips$log_tip<-log(tips$tip) tips$tip_percentage<-100*tips$tip/tips$total_bill
Variables:
We will examine the differences in tip, log_tip, tip_percentage and total_bill by entering them as outcomes. The factor is time. We will perform two types of tests on these variables, the t-test, and the brunner-munzel test (which is resistant to outliers). Additionally we will obtain unscaled plots by deselecting 'Scaled Variables"
descriptive.table(d(tip,log_tip,tip_percentage,total_bill),time,tips,func.names =c("Mean","St. Deviation","Valid N"))
print(two.sample.test(formula=d(tip,log_tip,tip_percentage,total_bill) ~ time,
data=tips,
test=t.test,
alternative="two.sided")
)
library(lawstat)
print(two.sample.test(formula=d(tip,log_tip,tip_percentage,total_bill) ~ time,
data=tips,
test=brunner.munzel.test,
alternative="two.sided")
)
oneway.plot(formula=d(tip,log_tip,tip_percentage,total_bill)~time,data=tips,
alpha=0.51))
> descriptive.table(d(tip,log_tip,tip_percentage,total_bill),time,tips,func.names =c("Mean","St. Deviation","Valid N"))
$`strata: Dinner `
Mean St. Deviation Valid N
tip 3.102670 1.4362428 176
log_tip 1.034377 0.4462253 176
tip_percentage 15.951779 6.7477139 176
total_bill 20.797159 9.1420292 176
$`strata: Lunch `
Mean St. Deviation Valid N
tip 2.7280882 1.2053454 68
log_tip 0.9201313 0.4004058 68
tip_percentage 16.4127928 4.0241549 68
total_bill 17.1686765 7.7138818 68
> print(two.sample.test(formula=d(tip,log_tip,tip_percentage,total_bill) ~ time,
+ data=tips,
+ test=t.test,
+ alternative="two.sided")
+ )
Welch Two Sample t-test
mean of Dinner mean of Lunch Difference 95% CI Lower 95% CI Upper t df
tip 3.102670 2.7280882 0.3745822 0.015053640 0.7341108 2.0593266 144.0712
log_tip 1.034377 0.9201313 0.1142453 -0.002574869 0.2310655 1.9341221 134.8400
tip_percentage 15.951779 16.4127928 -0.4610139 -1.850914865 0.9288870 -0.6540376 200.8764
total_bill 20.797159 17.1686765 3.6284826 1.331876787 5.9250885 3.1229862 143.2927
p-value
tip 0.041263422
log_tip 0.055192775
tip_percentage 0.513835616
total_bill 0.002166574
HA: two.sided
H0: difference in means = 0
> library(lawstat)
> print(two.sample.test(formula=d(tip,log_tip,tip_percentage,total_bill) ~ time,
+ data=tips,
+ test=brunner.munzel.test,
+ alternative="two.sided")
+ )
Brunner-Munzel Test
P(X<Y)+.5*P(X=Y) 95% CI Lower 95% CI Upper Brunner-Munzel Test Statistic df p-value
tip 0.4098429 0.3294411 0.4902447 -2.219022 126.3503 0.0282701762
log_tip 0.4098429 0.3294411 0.4902447 -2.219022 126.3503 0.0282701762
tip_percentage 0.5495906 0.4718788 0.6273023 1.260831 150.9286 0.2093154159
total_bill 0.3660177 0.2877780 0.4442575 -3.389074 125.3488 0.0009379292
> oneway.plot(formula=d(tip,log_tip,tip_percentage,total_bill)~time,data=tips,
+ alpha=0.51)
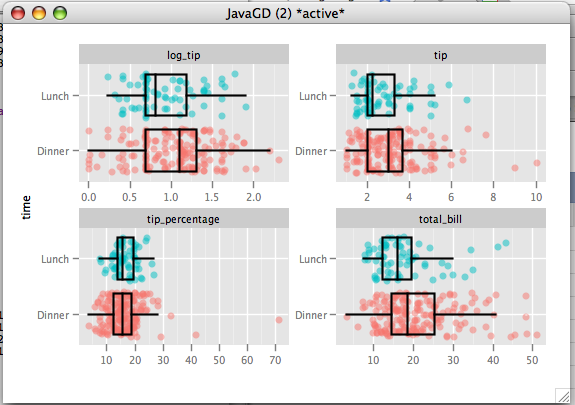
We can see from the plot that tip and total_bill are skewed, and tip_percentage has a number of large outliers (one party tipped 70%!!). We have a sample size of 244, which is fairly large, so we don't have to worry to much about the normality assumption. That said, due to their skew, comparing the means (as a t-test does) may not be the best method. The outliers in tip_percentage indicate that we should go with a robust method, at least for tip_percentage.
The brunner-munzel test, which compares central tendency (not means) and is robust to outliers, shows significance for tip (p=.028), log_tip(p=.028), and total_bill(p<.001). tip_percentage on the other hand is not significant (p=.209). From this we can conclude that dinner parties do tip more, and they have larger bills. They are not detectably more generous than the lunch customers because they tip a similar percentage of the bill.