Description
Performs a one sample t-test and/or normality test
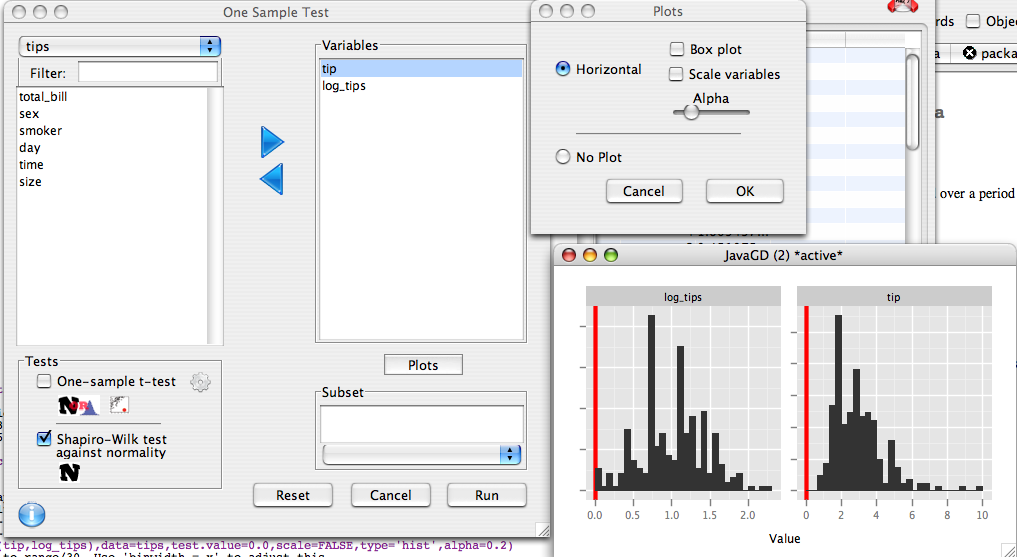
Dialog
Move all test variables from the left hand list to the variable list.
One Sample t-test
The one sample t-test tests whether the mean of a population is not equal to a specified value. For example, one might be interested to see if the mean weight change in a group of study participants is equal to zero. This test requires that either the sample size be sufficiently large, or the variable be normally distributed. 'Sufficiently large' in this case is fairly small for most distributions), as convergence of the test statistic to normality occurs rapidly. If outliers are present, this can lead to misleading inferences, so pre-screening of the data is recommended. The options button (the gear) allows for the specification of the alternate hypothesis and the null hypothesis mean.
Shapiro-Wilk Normality Test
This option performs the Shapiro-Wilk test against normality. This test determines if there is enough evidence to conclude that a variable in not normally distributed.
statistical advice: One common, though misguided technique is to pre-screen variables used in other parametric analyses using this test. For example, one might check the normality of the residuals of a regression as a diagnostic technique. Hypothesis testing is fundimentally the wrong tool to use. At small sample sizes normality hypothesis tests will be insignificant even in the presence of large deviations from normality due to lack of power. At large sample sizes, data that is nearly normal (nothing is ever exactly normal) will trigger a significant normality test because the test has the power to detect even the smallest deviations from normality. These are precisely the opposite types of miscategorizations that an analyst wishes to make. Most statistical tests are robust to large departures from normality provided the sample size is large enough. So normality matters most in the situations where you have no statistical power to detect it.
A better alternative to normality testing is to examine the histogram. Is it skewed or roughly symmetrical? Are its tails fat? If your sample is small and your variable is skewed you can try switching to non-parametric methods or transforming the variable so it looks more normal. Alternatively if you can program, you can run simulations to assess the procedure's sensitivity to departures from normality.
Plots
Two types of plots can be obtained through this dialog. If 'box plot is unchecked, a histogram is produced, otherwise, box and jitted plots are given. If 'Scale variables' is checked, all variables are standardized.
Examples
Normality test
One Sample t-test